yuns
Chapter 2 Properties of Networks, Random Graph Models 본문
Chapter 2 Properties of Networks, Random Graph Models
yuuuun 2020. 12. 19. 22:16Network Properties: How to Measure a Network
Plan: Key Network Properties
그래프 평가 요소
- Degree Distribution: $P(k)$
- Path length: $h$
- Clustering coefficient: $C$
- Connected components: $s$
1) Degree Distribution
- Degree Distribution $P(k)$: degree가 $k$개인 노드를 random하게 선택할 확률
- $N_k$: # of nodes with degree $k$
- Normalized histogram
- $P(k) = \frac{N_k}{N}$

2) Path in a graph
- path: 각 node가 다음 node에 연결되는 일련의 node
- $P_n = \{i_0, i_1, \cdots, i_n\}$, $P_n = \{(i_0, i_1), (i_1, i_2), \cdots, (i_{n-1}, i_n)\}$
- path는 자기자신을 intersect(교차)하여 edg를 여러번 통과 가능 (ex) ACBDCDEG

Distance in a Graph
- Distance(shortest path, geodesic)
- Between a pair of node: 최단 경로를 따르는 edge의 수

- B와 D의 distance: 2
- A와 X를 잇는 edge가 존재하지 않기 때문에 Infinite 값으로 정의
- smallest possible sum of the edge weights that gets between the two nodes
- Directed Graph에서 path는 화살표의 direction을 따라야 함
- distance is not symmetric!!
Network Diameter
graph가 얼마나 큰지
- Diameter: graph에서 node 쌍 사이의 최대 거리 (잘 사용하지 않음)
- Average Path Length: Path Length의 평균값
3) Clustering Coefficient
undirected graph에서만 정의되어 있음
- How connected are $i$'s neighbors to each other?
- 친구들끼리 얼마나 서로 잘 아는가에 대해서 알기 위함
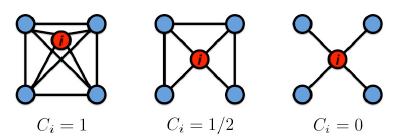
- 제일 왼쪽에 있는 그래프가 모든 node에 대하여 연결되어 있기 때문에 서로를 제일 잘 안다고 할 수 있음
- Clustering Coefficient는 모든 node에 대하여 계산
- $C_i = \frac{2e_i}{k_i(k_i -1)}$ where $C_i \in [0, 1]$
- $e_i$: the number of edges between the neighbors of node $i$
- node $i$와 연결되어 있는 노드들간의 연결된 edge의 개수
- $\frac{k_i(k_i-1)}{2}$가 degree의 개수가 주어질 경우 생성될 수 있는 총 edge의 개수를 의미
- 두 번째 그래프의 경우, $e_i = 3, k_i = 4$ 로 계산
- $C_i = \frac{2e_i}{k_i(k_i -1)}$ where $C_i \in [0, 1]$
- Average Clustering coefficient $C = \frac{1}{N} \sum_i^N C_i$
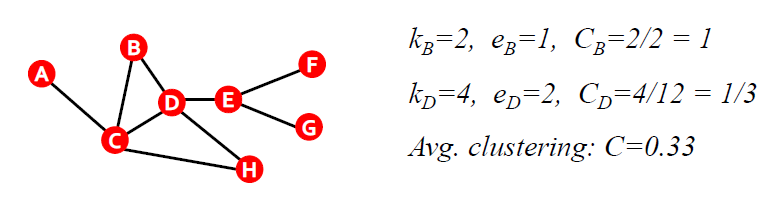
4) Connectivity
size of the largest connected component

Erdos-Renyi Random graph Model
Simplest Model of Graphs
node의 개수인 n과 친구를 맺을 확률인 $p$가 정해지면 그래프를 생성해줌
2 variants
- $G_{np}$: n개의 node를 가지는 undirected graph에서 임의의 두 node $u, v$사이의 edge인 $(u, v)$가 p의 확률을 가질 경우
- $G_{nm}$: n개의 node를 가지는 undirected graph 에서 m개의 edge들이 uniformly random하게 뽑힐 경우
What kind of networks do such models produce?
Random graph Model
- $n$ and $p$ do not uniquely determine the graph
- graph는 random process의 결과
Properties of $G_{np}$
Degree distribution: $P(k)$
Path Length: $h$
Clustering coefficient: $C$
What are the values of these properties for $G_{np}$?
1) Degree Distribution
- Degree Distribution of $G_{np}$ is binomial(이항분포)
- $P(k)$: fraction of nodes with degree $k$

- mean $k = p(n-1)$
- variance $\sigma ^2 p(1 - p)(n - 1)$
- graph가 커지게 되면 이항분포의 폭이 좁아짐
2) Clustering Coefficient of $G_{np}$
자신의 neighbor들끼리 서로 얼마나 아는지에 대하여 표현
- $C_i = \frac{2e_i}{k_i(k_i - 1)}$
- Edges in $G_{np}$ appear independent identically distributed with probability $p$


3) Path Length(Diameter)
Expansion $\alpha$: 전체 노드를 두 영역으로 나눌 때, 작은 영역에서 큰 영역으로 가는 edge의 최소값
Path Length: $O(\log n)$
- if $\forall_{S\subseteq V}$: $ of edges leaving $S \geq \alpha min(|S|,|V\S|)$

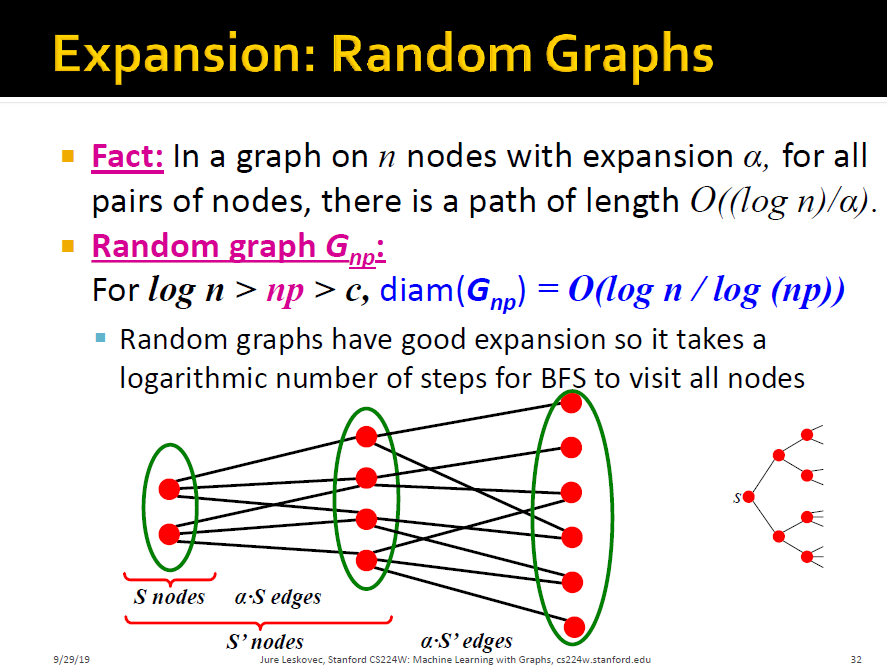
4) Connectivity

n이 1보다 클 때부터 폭발적으로 증가함을 볼 수 있음
Back to MSN vs $G_{np}$

Real Networks vs $G_{np}$


random graph의 경우 node의 개수가 커지면 Clustering Coefficient가 낮아지고 Degree Distribution의 분포가 다르기 때문에 real world를 묘사하는데 무리가 있음
현실적으로 k에 따른 $p(k)$가 정규 분포를 따르지 않는다는 단점이 존재
이항분포를 목표로 하지만 실질적으로 power law distribution을 따르게 된다.
The Small-World Model
Can we have high clustering while also having short paths?
Controversy
Consequence of expansion
- Short paths: $O(log n)$
- smallest diameter we can get if we keep the degree constant
Social Network는 일반적으로 "local" structure를 가지고 있음
- Triadic closure: 친구의 친구도 내 친구임! (clustering이 높을 것임)
- 낮은 diameter를 가지면 낮은 cluster를 가지게 됨

일반적으로 high clustering과 small diameter인 network를 가지고 싶은데 두 개를 동시에 만족할 수 없는 단점 발생
Small-World : How?
High clustering을 가지는 network가 small world(small diameter)일 수 있나? ($\log n$ diameter)

Watts-Strogatz Model
랜덤하게 뽑은 시작 노드와 연결되어 있는 edge를 하나 뽑아서 end node로 edge를 연결함으로써 rewire함
Two components to the model
- Start with a low-dimensional regular lattice
- 높은 clsutering coefficient
- Rewire: randomness("shortcuts")
- edge를 더하거나 없앰


정리
- clustering과 small-world간의 상호작용에 대한 통찰력 제공
- 실제 네트워크의 구조 탭처
- 실제 네트워크의 높은 clustering의 설명
- 정확한 degree-distribution으로 이어지지 않음 (단점)
Kronecker Graph Model
Idea: Recursive Graph Generation
How can we think of network structure recursively? (Self-Similarity)
- object가 자신의 일부와 유사하다는 특징을 이용하여 전체가 하나 이상의 부분과 동일한 모양을 가진다.

Kronecker product는 self-similar matrices를 생성하는 방법
Kronecker Graph [PKDD '05]

Kronecker Product
B의 그래프를 A의 요소만큼 곱하고 그를 반복하는 것

이를 adjacency matrix로 정의함


Stochastic Kronecker Graphs
- Create $N_1 \times N_1$ probability matrix $\theta _1$
- Compute the $k^{th}$ Kronecker power $\theta _k$
- 각 $\theta _k$ 의 entry인 $p_{uv}$은 edge (u, v)를 $p_{uv}$ 의 확률로 $K_k$에 포함하고 있음




Generation of Kronecker Graphs


'[CS224W] Machine Learning with Graphs' 카테고리의 다른 글
| 2020-01 Intro (0) | 2021.06.14 |
|---|---|
| Lecture 3 Motifs and Structural Roles in Networks (0) | 2020.12.29 |
| Lecture 3 Motifs and Structural Roles in Networks (0) | 2020.12.20 |
| Lecture 1 Introduction - Structure of Graphs (0) | 2020.12.19 |




