paper study/graph
Markov Decision Process
yuuuun
2020. 12. 13. 12:13
반응형
강화학습은 MDP의 문제를 푸는 것
https://sumniya.tistory.com/3 참조
Markov Process의 정의
- 확률론에서 Markov Process는 메모리를 갖지 않는 이산 시간 확률 과정
- 확률 과정: 시간이 진행함에 따라 상태가 확률적으로 변화하는 과정
- 확률 분포를 따르는 random variable 가 discrete한 time interval 마다 값을 생성해내는 것을 의미
- time interval이 discrete하고 현재의 state가 이전 state에만 영향을 받는 확률 과정을 Markov Process라 함
Markov Property
- 어떤 시간에 특정 state를 도달하든 그 이전에 어떤 state를 거쳐왔든 다음 state로 갈 확률은 항상 같다
- $Pr(S_{t+1} = s' | S_0, S_1, \cdots, S_{t-1}, S_t) = Pr(S_{t+1} = s' | S_t)$
- 0 ~ t시간 까지의 여러 state를 거쳐오고 (t+1) 시간에 s'라는 state에 도달할 활귤이 바로 직전 t시간의 state에서 state $s'$로 올 확률은 같다.
State Transition Probability Matrix
- State들 간에 이동하는 것을 transition이라 하며 이를 확률로 표현
- state transition probability: $P_{ss'} = Pr(S_{t+1} = s' | S_t = s)$
Markov Reward Process(MRP)
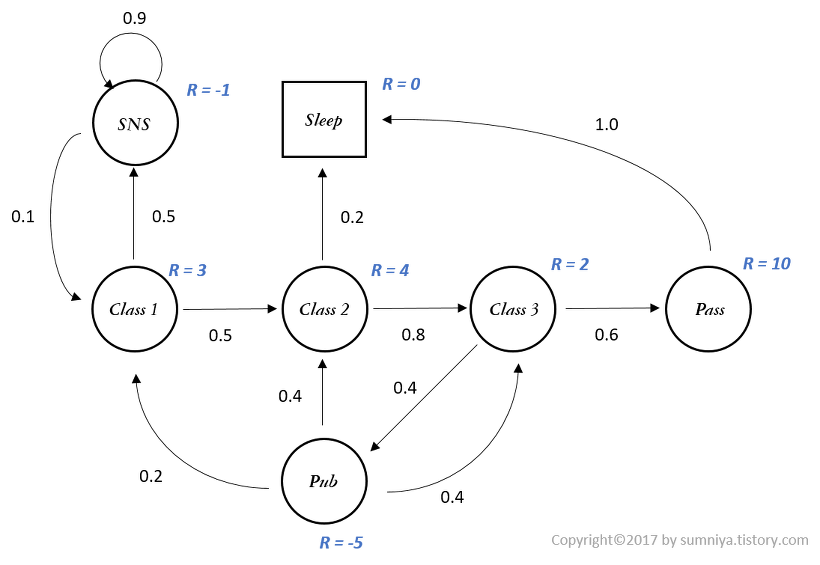
- Markov Process에 Reward의 개념을 추가한 것
- 현재 state에서 다음 state로 가는 것이 얼마나 가치있는지 알기 위하여 도입한 Reward의 개념
- $R_s = E[r_{t+1} | S_t = s]$: state를 받아 reward의 기대값으로 mapping하는 함수
- 바로 다음 시간인 (t+1)에 얻을 수 있는 보상이기 때문에 immediate reward라 함
Discounting Factor
- 현재의 state의 정확한 가치를 구하기 위해서 어느 시점에서 reward를 얻는 시점이 중요
- discounting factor $\gamma$ 는 [0, 1]의 값으로 미래가치를 현재 시점에서의 가치로 변환
Return
- 먼 미래에 얻을 수 있는 total reward에 대해 고려하게 되고 이를 Return이라 함 $$G_t = R_{t+1} + \gamma R_{t+2} + \cdots = \sum_{k=0} ^\infty \gamma^k R_{t+k+1}$$
- $R$: immediate reward로서 현재가치로 환산하여 합한 것
Value Function of MRP
- state의 가치를 표현하는 함수를 Value Function
- 어떠한 state에서 미래를 얻을 수 있는 모든 reward를 더한 것의 expectation $$V(s) = E[G_t | S_t = s]$$
- state s 에서 이동 가능한 state들의 scenario들을 따라 그 state들의 reward에 discounting factor를 적용하여 모두 더한 값이 state s에서의 가치 $V(s)$.
Markov Decision Process(MDP)
MP + reward = MRP, MRP + action = MDP
Action
- state에서 action을 하여 state가 변함
Policy
- state에서 action을 mapping하는 함수
- 해당 state에서 어떤 action을 할 지를 정하는 것을 policy라 함 $$\pi (a | s) = Pr(A_t = a | S_t = s)$$
Value Function of MDP
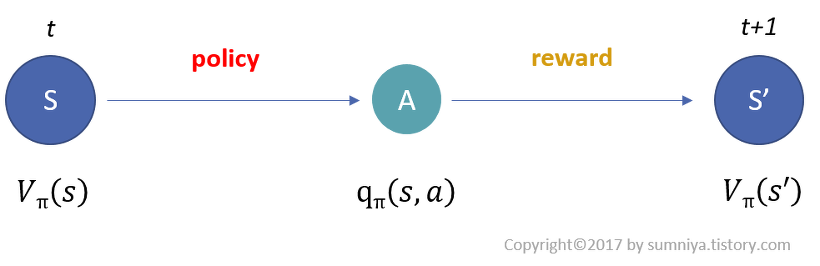
- MDP의 process
- t시점에 state s에 놓인 agent가 policy에 따라 action a 수행
- state s에서 action a를 수행하면 reward를 받음
- transition probability에 따라 state s'로 전이
- State-Value Function
- state에서 선택하는 policy에 따라 그 action이 달라지고 이후 state가 달라지기 때문에 policy에 영향을 받음 $$V_\pi (s) = E_\pi [G_t | S_t = s]$$
- MDP에서 state s의 가치는 해당 state에서 policy에 얻게 되는 reward들의 총합(return)을 나타냄
- Action-Value Function
- agent가 하는 action에 대하여 value를 판단 $$q_\pi (s, a) = E_\pi [G_t | S_t = s, A_t = a]$$
- action a의 가치는 State s 에서 policy에 따라 action을 취했을 때, 얻게 되는 reward들의 총합을 나타냄
반응형